On a Third Order CWENO Boundary Treatment with Application to Networks of Hyperbolic Conservation Laws

by Alexander Naumann, Oliver Kolb, Matteo Semplice.
Paper    arXiv    Venue    Notes   

© 2018, Elsevier Inc.

Abstract

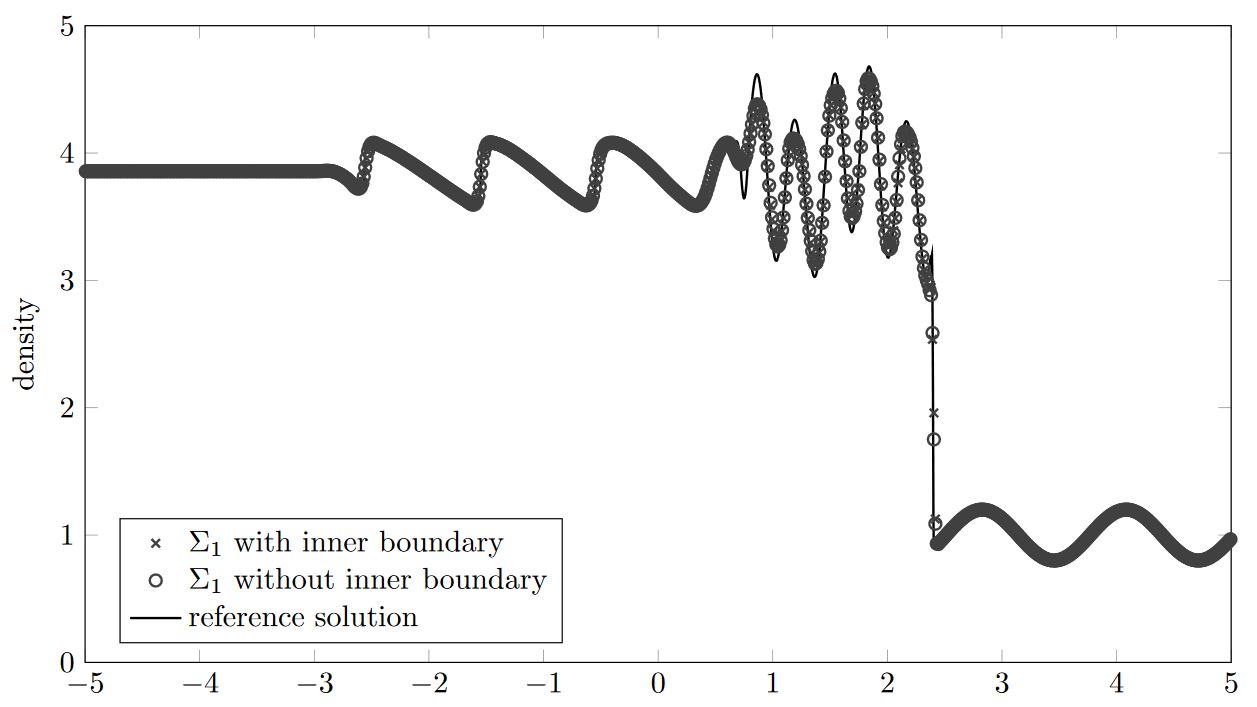
High order numerical methods for networks of hyperbolic conservation laws have recently gained increasing popularity. Here, the crucial part is to treat the boundaries of the single (one-dimensional) computational domains in such a way that the desired convergence rate is achieved in the smooth case but also stability criterions are fulfilled, in particular in the presence of discontinuities. Most of the recently proposed methods rely on a WENO extrapolation technique introduced by Tan and Shu (2010). Within this work, we refine and in a sense generalize these results for the case of a third order scheme. Numerical evidence for the analytically found parameter bounds is given as well as results for a complete third order scheme based on the proposed boundary treatment.